前言

在学校信息队训练的时候布置了这一道题目，但是只求一次。然后上洛谷发现 UVA 题库求多次，因为方法一样只需嵌套，所以就做了一下（没有账号提交不了 = m=）

信息队原题

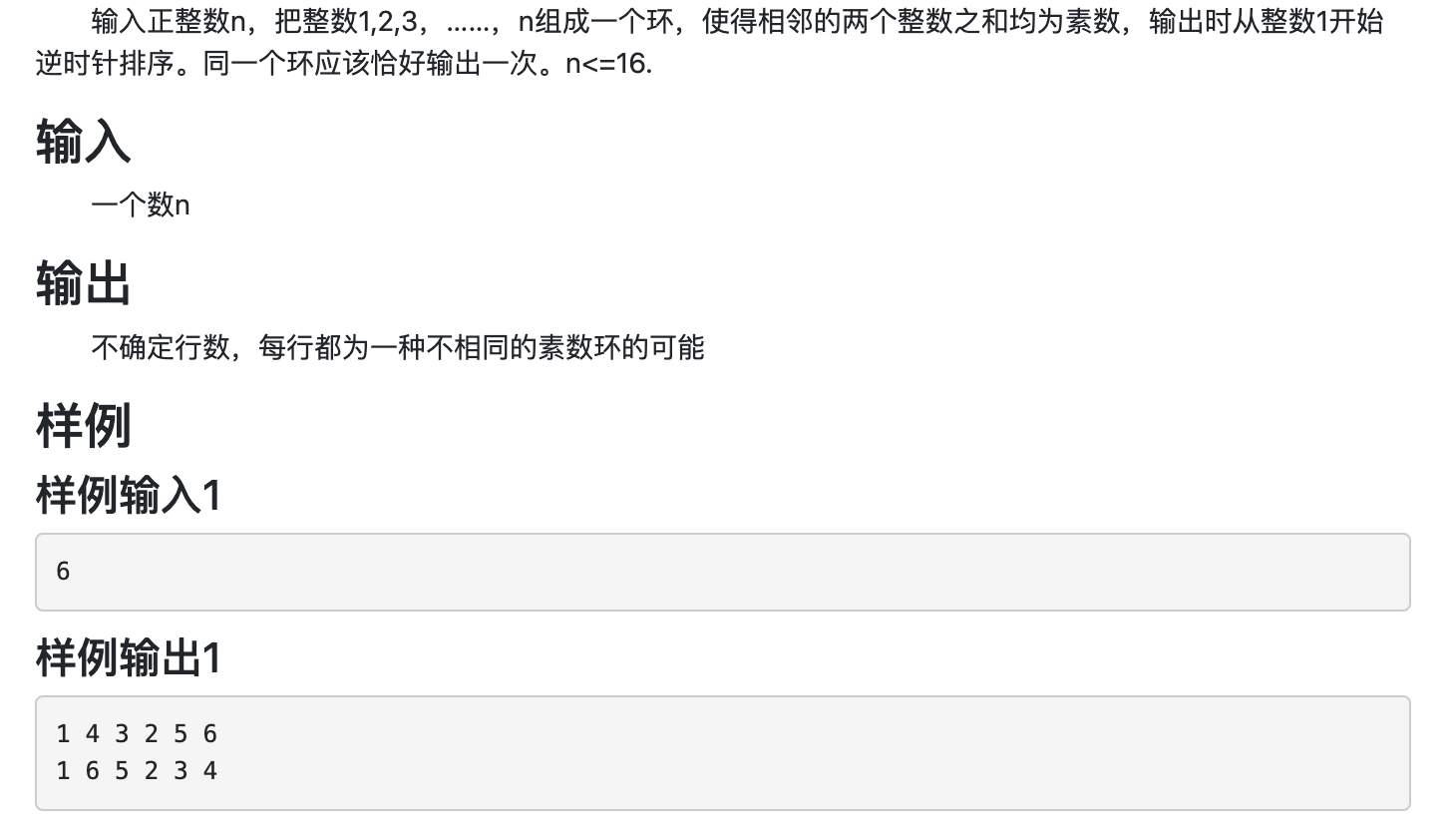
1. 题目分析

题目要求将整数 到 组成一个环，使得相邻的两个整数之和均为素数。

我们需要找到所有满足条件的素数环，并按照要求输出。

由于 的值不超过 ，我们可以使用回溯法来尝试所有可能的组合。

2. 做题思路

判断当前取出的数字是否和前一个组成素数，这一步可以用一个 check 函数来解决（num 的值为两个数字的和）

bool check(int num)
{
    if (num < 2)
    {
        return false;
    }
    for (int i = 2; i * i <= num; i++)
    {
        if (num % i == 0)
        {
            return false;
        }
    }
    return true;
}

在创建一个 back 函数用于回溯：

void back(int cur)  // cur 表示当前位置
{
    if (cur == n)  // 检查最后一个数字和第一个数字之和是否为素数
    {
        if (check(arr[0] + arr[n - 1]))
        {
            for (int i = 0; i < n; i++)
            {
                cout << arr[i] << " ";
            }
            cout << endl;
        }
        return;
    }
    for (int i = 2; i <= n; i++)
    {
        if (!vis[i] && check(arr[cur - 1] + i))
        {
            vis[i] = true;
            arr[cur] = i;
            back(cur + 1);
            vis[i] = false;
        }
    }
}

在 back 函数中，首先判断是否已经放置了 个数字。如果是，则检查最后一个数字和第一个数字之和是否为素数。如果是素数，则输出这个环。

然后，从数字 到 依次尝试将每个数字放在环的下一个位置。如果该数字没有被使用过，并且与前一个数字之和为素数，就将其放在环的下一个位置，并标记为已使用，然后继续递归放置下一个数字。

如果放置过程中出现相邻两个数字之和不是素数的情况，就回溯到上一个数字，重新选择下一个数字。

最后是 main 函数，在 main 函数中，读取输入的 ，初始化标记数组和环的第一个数字，然后调用 back 函数从数字 开始回溯。

3. 复杂度计算

时间复杂度：由于需要尝试所有可能的组合，时间复杂度为 ，其中 n 是输入的数字个数

空间复杂度：主要是使用了标记数组和环数组，空间复杂度为

4. 完整代码

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 16;
int n;
int arr[MAXN];
bool vis[MAXN];

// 判断一个数是否为素数
bool check(int num)
{
    if (num < 2)
    {
        return false;
    }
    for (int i = 2; i * i <= num; i++)
    {
        if (num % i == 0)
        {
            return false;
        }
    }
    return true;
}

// 回溯
// cur表示当前位置
void back(int cur)
{
    if (cur == n)  // 检查最后一个数字和第一个数字之和是否为素数
    {
        if (check(arr[0] + arr[n - 1]))
        {
            for (int i = 0; i < n; i++)
            {
                cout << arr[i] << " ";
            }
            cout << endl;
        }
        return;
    }
    for (int i = 2; i <= n; i++)
    {
        if (!vis[i] && check(arr[cur - 1] + i))
        {
            vis[i] = true;
            arr[cur] = i;
            back(cur + 1);
            vis[i] = false;
        }
    }
}

int main()
{
    cin >> n;
    memset(vis, false, sizeof(vis));
    vis[1] = true;
    arr[0] = 1;
    back(1);
    return 0;
}

洛谷 UVA 题库版

前面不是说了吗，UVA 也有一个版本，是给出多个值，这里给出题目：

其实就是多次输入，用 while 循环解决，终止条件为 n == EOF，所以可以这样写。

while(n != EOF)
{
    cin >> n;
    memset(vis, false, sizeof(vis));
    vis[1] = true;
    arr[0] = 1;
    back(1);
}

现在是把刚才信息队版本的输入和操作套在了循环里，这就完了，是不是很简单？

其实没完，题目中说要在第 i 行添加上 Case i ，所以再搞一个变量就完事了！

int idx = 1;  // 此处 idx 变量即 i 变量
while(n != EOF)
{
    cin >> n;
    cout << "Case " << idx++ << ":" << endl;  // 输出 Case i 因为 "++" 在后是先赋值再运算，所以可以这么写，就相当于先输出 idx 当前值再加
    memset(vis, false, sizeof(vis));
    vis[1] = true;
    arr[0] = 1;
    back(1);
}

最终代码

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 16;
int n;
int arr[MAXN];
bool vis[MAXN];

// 判断一个数是否为素数
bool check(int num)
{
    if (num < 2)
    {
        return false;
    }
    for (int i = 2; i * i <= num; i++)
    {
        if (num % i == 0)
        {
            return false;
        }
    }
    return true;
}

// 回溯
// cur表示当前位置
void back(int cur)
{
    if (cur == n)  // 检查最后一个数字和第一个数字之和是否为素数
    {
        if (check(arr[0] + arr[n - 1]))
        {
            for (int i = 0; i < n; i++)
            {
                cout << arr[i] << " ";
            }
            cout << endl;
        }
        return;
    }
    for (int i = 2; i <= n; i++)
    {
        if (!vis[i] && check(arr[cur - 1] + i))
        {
            vis[i] = true;
            arr[cur] = i;
            back(cur + 1);
            vis[i] = false;
        }
    }
}

int main()
{
    int idx = 1;
    while(n != EOF)
    {
        cin >> n;
        cout << "Case " << idx++ << ":" << endl;
        memset(vis, false, sizeof(vis));
        vis[1] = true;
        arr[0] = 1;
        back(1);
    }
    return 0;
}

写在最后

到这里本片题解就结束了，UVA 版本没提交，前面说了注册不起账号，但是代码应该没问题，有问题评论告知，谢谢支持🙏